如何計算電路功率因數，計算公式是怎么樣的，在計算功率因數時，注意功率因數與位移因數的區別，介紹了正弦電路功率因數符號和功率因數計算公式，非正弦電路功率因數符號和功率因數計算公式。

電路功率因數符號和功率因數計算公式

自從交流電機取得應用至今日，功率因數和位移因數在很多場合被混淆。很多人都把功率因數誤認為就是cosφ，并用cosφ作為功率因數符號。

并以此為基礎，得出有功功率P、無功功率Q和視在功率S之間的直角三角形關系。即：

P=S*cosφ （1）

Q=S*sinφ （2）

S2=P2+Q2（3）

功率因數（Power Factor，縮寫為PF）表示有功功率與視在功率的比值，常用λ表示，功率因數計算公式如下：

λ=P/S

視在功率定義為電壓有效值U與電流有效值I的乘積，用S表示，基本單位為VA，即S=UI。視在功率也稱表觀功率。

視在功率計算公式如下：

S=UI （4）

有功功率定義為瞬時功率在一個周期內的積分的平均值，用P表示，基本單位為W，假設交流電周期為T，電壓、電流的瞬時值表達式分別為u(t)、i(t)，有功功率計算公式如下：

（5）

有功功率也稱平均功率。

上述視在功率計算公式（4）和有功功率計算公式（5）在任何情況下均能成立。

1、正弦電路功率因數符號和功率因數計算公式

在正弦穩態電路中，根據有功功率計算公式（5），可以推導出下述簡化的有功功率計算公式：

P=UIcosφ。 （6）

φ為正弦電壓、電流的相位差。

將視在功率計算公式（4）代入正弦電路有功功率計算公式（6），可得到本文開始時提出的式（1）。

式（1）只有在正弦穩態電路中才能成立。即：在正弦穩態電路中，功率因數數值上等于位移因數cosφ。由于正弦電路是交流電路的基礎，且電網的電壓波形為正弦波，早期大部分用電器為線性負載，電流波形也是正弦波。因此，大家習慣了用cosφ作為功率因數符號。

2、非正弦電路功率因數符號和功率因數計算公式

隨著電力電子技術的發展變頻器、整流器等非線性設備得到廣泛的應用功率因數計算公式，非線性設備的特點是，即便采用正弦電壓供電，其電流也不是正弦波。另外，電網諧波污染日益嚴重，電網電壓的非正弦性（波形畸變率）日益嚴重。

只要電壓和電流兩者中有一個或一個以上為非正弦波，式（1）就不再成立，功率因數符號也就不能用cosφ表示。

根據傅里葉變換理論，非正弦交流電量可以分解為基波及頻率為基波頻率整數倍的諧波的線性組合。而有功功率P就等于基波及各次諧波相互作用的有功功率之和。

根據三角函數正交性理論，不同頻率的正弦波相互作用功率因數計算公式，不產生有功功率。

因此，通用有功功率計算公式（5）可以用下述形式表示：

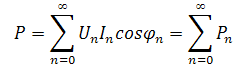
（7）

式中，n=0、1、2...

U0、I0表示直流分量，U1、I1表示電壓、電流基波有效值。P0表示直流功率，P1表示基波有功功率。

Un、In表示n次諧波電壓和諧波電流的有效值，Pn表示n次諧波電壓與n次諧波電流作用下的n次諧波有功功率。

φ0=90°，φ1表示基波電壓與基波電流的相位差，φn表示n次諧波電壓與n次諧波電流的相位差，

cosφ1稱為基波功率因數或位移因數。

類似的，視在功率表示為：

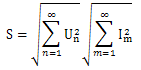
（8）

由有功功率計算公式（7）和視在功率計算公式（8）可得適用非正弦電路的下述功率因數計算公式：

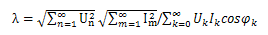
（9）

盡管非正弦電路中，cosφ已經不再等于功率因數，然而，由于長期以來人們習慣了用cosφ作為功率因數符號。因此，在某些特殊的非正弦電路中，功率因數的表達方式仍采用類似的形式表示。

特例1：

電網供電的非線性設備，對于精度要求不高的場合，可認為電網電壓為正弦波。由于是非線性設備，其電流為非正弦波。

根據三角函數正交理論，有功功率計算公式如下：

P=∑Pn=P1=U1I1cosφ1=UI1cosφ1

功率因數計算公式可簡化為：

λ=P/S=(I1/I)cosφ1 （10）

I1/I為電流畸變因數。即功率因數受位移因數和電流畸變因數兩部分的影響。

特例2：

PWM變頻器供電的電機的供電電壓為非正弦波，電流接近正弦波。對于精度要求不高的場合，可以認為電流為正弦波。

與特例1類似，變頻器輸出功率因數計算公式可簡化為：

λ=P/S=(U1/U)cosφ1 （11）